Game theory is the study of rational behavior in situations involving interdependence. Game Theory is a formal way to analyze the interaction among a group of rational individuals who behave strategically. Originally, it addressed zero-sum games, in which one person’s gains result in losses for the other participants.
A rational individual takes action that is consisted of his or her goals. Interdependence means that any player is affected by what others do and his actions must depend on the prediction of others’ responses. For an individual to decide what to do, they must determine how are others are going to act. This determination requires knowledge of other’s aims as well as the options available to them.
Game Theory has been used to make decisions on price, output, product development, product promotion and other business scenarios.
Game Theory Examples
- Buyers and sellers negotiating a price
- Firm and its competitors
- Auctions
- Prisoner’s Dilemma
Cooperation in game theory is usually analyzed by means of a non-zero-sum game called the Prisoner’s Dilemma. It was originally framed by Merrill Flood and Melvin Dresher working at RAND in 1950. Albert W. Tucker formalized the game with prison sentence rewards and named it, “Prisoner’s Dilemma”.
Two members of a criminal gang are arrested and imprisoned. Each prisoner is in solitary confinement with no means of communicating with the other. The prosecutors lack sufficient evidence to convict the pair on the main charge. They hope to get both sentenced to a year in prison on a lesser charge. Simultaneously, the prosecutors offer each prisoner a bargain. Each prisoner is given the opportunity either to: betray the other by testifying that the other committed the crime, or to cooperate with the other by remaining silent. The offer is:
- If A and B each betray the other, each of them serves two years in prison
- If A betrays B, but B remains silent, A will be set free, and B will serve three years in prison (and vice versa)
- If A and B both remain silent, both of them will only serve one year in prison (on the lesser charge)
The two players in the game can choose between two moves, either “cooperate” or “defect.” The idea is that each player gains when both cooperate, but if only one of them cooperates, the one who defects, will gain more. If both defect, both lose.
The Prisoner’s Dilemma Example
The table below shows the payoffs for a Prisoner’s Dilemma game.
Economists consider Prisoner’s Dilemma games to be zero-sum in that there is no cooperation: either each gets 0 when both defect, or when one of them cooperates, the defector receives (+10), and the cooperator (-10), a total of 0.
If both cooperate, there will be a positive gain: each of them gets 5, a total of 10. The gain for cooperation (5) is smaller than the gain for one-sided defection (10) so that there is always a temptation to defect.
| Action of A / Action of B | Cooperate | Defect |
|---|---|---|
| Cooperate | Fairly Good (+5) | Bad (-10) |
| Defect | Good (+10) | Mediocre (0) |
Sequential Move Games
The Prisoner’s Dilemma game is a game in which both players move simultaneously. There is another type of game where players make their moves in specific sequences called Sequential Move Games.
Sequential Move Game Example
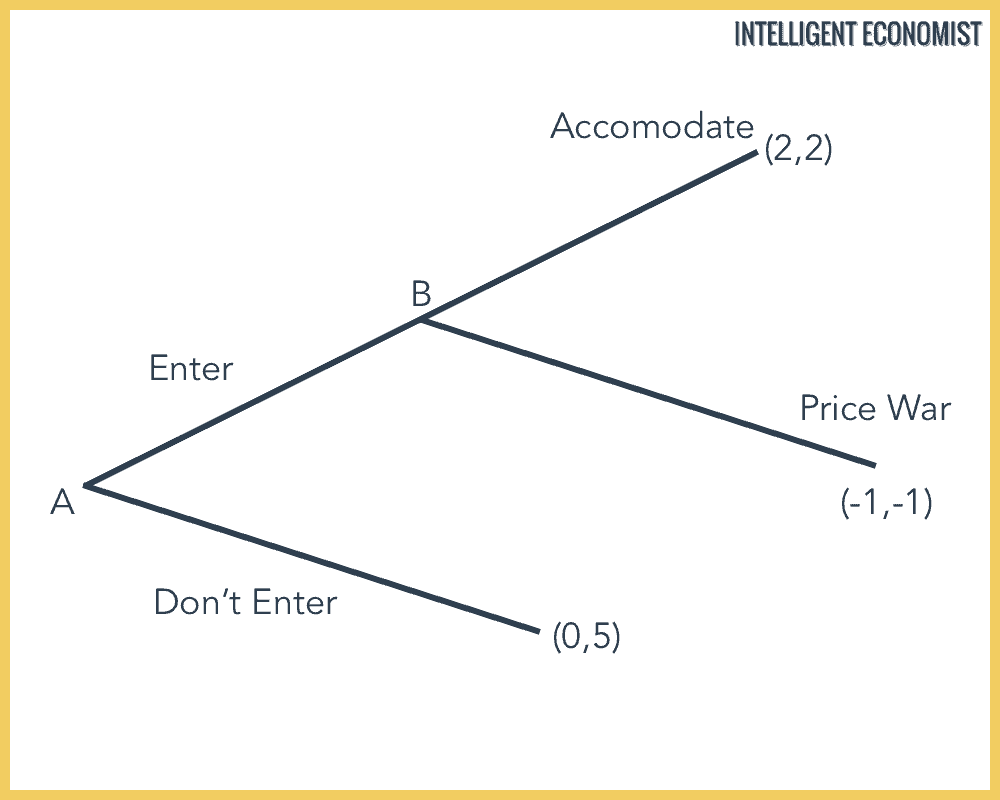
In this Sequential Move Game, Player A is a new entrant into a market. He has two choices:
He can either enter the market or stay out.
Player B is already in the market, and if player A enters, he has the choice either to accommodate his competitor and not raise prices or to start a price war.
The logical move for player A would be to enter the market because he knows that if he does join, player B will choose ‘accommodate’ and receive a payoff of (1), rather than try to start a price war and get (-1).
For player A, a payoff of (1) is better than (0), the payoff for staying out of the market.
Nash Equilibrium
The Nash equilibrium was named after John Forbes Nash, Jr. A Nash Equilibrium occurs when a player plays optimally and correctly guesses what the other player will do. In other words, each player plays a best-response strategy by assuming the other player’s moves. In the Nash Equilibrium, each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only their own strategy.
Nash Equilibrium Example
A Coordination Game:
| Left | Right | |
|---|---|---|
| Up | -1, -1 | 2, 0 |
| Down | 1, 1 | 1, 1 |
Player 1: If Player 1 assumes Player 2 will choose Left, Player 1 will choose Down
If Player 1 assumes Player 2 will choose Right, Player 1 will choose Up
Player 2: If Player 2 assumes Player 1 will choose Up, Player 2 will choose Right
If Player 2 assumes Player 1 will choose Down, Player 2 will be indifferent to Left or Right
It is easy to determine that this game has two Nash Equilibriums at (Down, Left) and (Up, Right). Both of these strategies contain payoffs that are both best responses for each player.

