Decision-making under uncertainty is a complex topic because all decisions are made with some degree of uncertainty. But there are specific scenarios in which economic experiments have shown that some people make decisions deviating from expected utility theory defined by the Von Neumann-Morgenstern theorem. While the experiments are conducted under certain restrictions, the findings can be and have been extended to many relevant real-world scenarios.
Von Neumann-Morgenstern Expected Utility Theory and Risk Preferences
When thinking about decisions involving uncertainty, the von Neumann-Morgenstern utility function must first be discussed since it describes how rational agents should theoretically act when facing a decision. The function arises from the expected utility hypothesis and “shows that when a consumer is faced with a choice of items or outcomes subject to various levels of chance, the optimal decision will be the one that maximizes the expected value of the utility (i.e. satisfaction) derived from the choice made.” It relies on assumptions of completeness (that a decision can always be made), transitivity (consistent choices in different scenarios), independence (an irrelevant choice won’t change anything), and continuity (there are possible combinations of probabilistic choices that lead to indifference).
This theory drove the classification of agents as risk-averse, risk-neutral, and risk-loving. These classifications are referred to as risk preferences, and they inform economic analyses by categorizing agents into certain groups.
Risk-averse agents are those that dislike uncertainty – they would rather have a lower payoff with more certainty than a higher payoff with more uncertainty.
A risk-neutral agent is indifferent between choices with differing levels of uncertainty as long as the expected value is equal.
A risk-loving (or risk-seeking) agent would prefer a higher payoff with more uncertainty over a lower payoff with more certainty.
An agent’s behavior can often be predicted based on their classification as risk-averse, -neutral, or -loving. However, deviations from the expected behavior create interesting scenarios and theories and are the focus of the rest of this article.
St. Petersburg Paradox
The St. Petersburg Paradox is one of the most interesting examples of Decisions Involving Uncertainty. The paradox was first described by Daniel Bernoulli. The St. Petersburg Paradox says that a rational investor should be willing to pay an infinite amount of money for the following game:
If a coin is flipped and it comes up heads, the investor is paid $1. If it’s flipped again and it comes up heads again, the investor gets $2. If it comes up heads a third time, $4; a fourth time $8; and so on. Once tails comes up the game is over. So, the total prize is $2n, where n is the total number of flips.
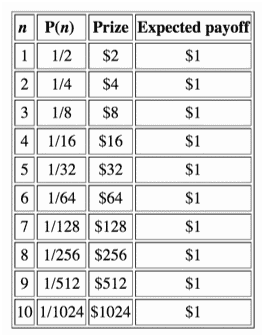
The chart above (from an article in the Stanford Encyclopedia of Philosophy) summarizes the payoff structure for a sample of 10 flips, where P(n) indicates the probability of getting that many heads in a row. Since there is an infinite number of possible consequences and each has an expected payoff of $1, the sum of the expected payoffs is infinity. And the rational investor should be willing to pay an infinite amount to play this game.
However, an investor would not really pay an infinite amount of money to play this game, even if that was technically possible. It’s commonly thought that people would pay about $20-$25 to play.
Bernoulli describes this deviation from theoretical behavior by saying that “mathematicians evaluate money in proportion to its quantity [the expected value here] while, in practice, people with common sense evaluate money in proportion to the utility they can obtain from it.” In other words, people don’t expect to get an infinite amount of money in reality, so they’ll only be willing to make a small investment to potentially earn a reasonable profit (that they could then realistically use).
Risk aversion may also play a part in describing why people won’t pay an infinite sum in practice to play the game. “Very low payments are very probable, and very high ones very rare. It’s a foolish risk to invest more than $25 to play … many of us are risk-averse, and unwilling to gamble for a very small chance of a very large prize” (Stanford Encyclopedia). While risk aversion doesn’t explain everything, it provides a reasonable starting point for an explanation of why some people won’t play for any amount of money.
Allais Paradox
The Allais paradox is another surprising example of how people deviate from expected utility theory. The classic experiment to demonstrate this paradox is shown below. People are asked to choose between A and B in each experiment independently. Think about what you might choose before reading on.
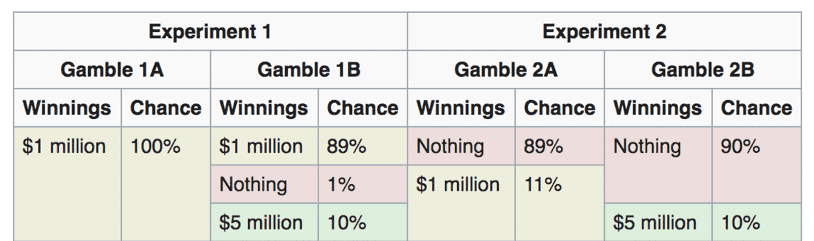
Many people choose 1A and 2B, which are both reasonable choices if people were only asked about each experiment individually. But choosing them together violates expected utility theory (i.e. theoretically rational agents would choose 1A and 2A or 1B and 2B). The reason is that “in expected utility theory, equal outcomes added to each of the two choices should have no effect on the relative desirability of one gamble over the other; equal outcomes should ‘cancel out’.” See the choices described this way below.
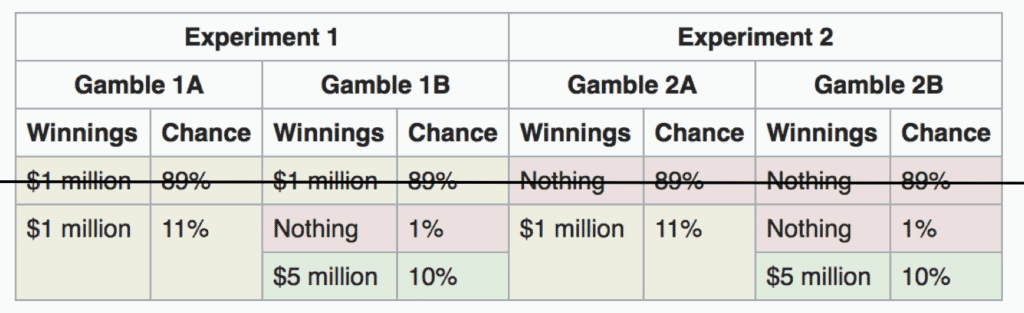
Really nothing has changed here; the only thing is that the $1 million in gamble 1A is split into an 89% chance and an 11% chance of getting $1 million (in other words, still a 100% chance of getting $1 million). Then the first row can be eliminated because the choices are the same between gambles for each experiment. Seeing the choices described this way shows that it would actually be rational to choose 1A and 2A or 1B and 2B (depending on one’s risk preferences) because they’re the same choices. This paradox shows that people who choose 1A and 2B together violate the independence axiom of expected utility theory because the addition of an irrelevant choice (89% chance of $1 million or 89% chance of nothing) would change their decision.
Ellsberg Paradox
Another paradox is the Ellsberg paradox, which was first identified by Daniel Ellsberg in 1961. Essentially, the paradox shows that people more often than not tend to prefer situations where they know the risk.
For example, if the two options are a 10% chance of winning versus and an unknown chance of winning (that is actually a 90% chance of winning), people would choose the 10% chance because there is the possibility that the unknown chance of winning is 0%. This phenomenon is often simply described as preferring the ‘devil you know’ over the one you don’t.
Ellsberg illustrates this paradox with a choice game. In the scenarios, there is one urn containing 30 red balls and one containing 60 black and yellow balls of unknown proportions (i.e. there could be 60 black balls and 0 yellow, 60 yellow and 0 black, or any combination in between).
In scenario 1, the agent must guess whether a red ball or a black ball will be pulled out of the urn. In scenario 2, the agent must choose between one of the following options: that 1) either a red or a yellow will be pulled out of the urn, or that 2) either a black or yellow will be pulled out. In both scenarios, the prize for choosing the correct ball color is $100.
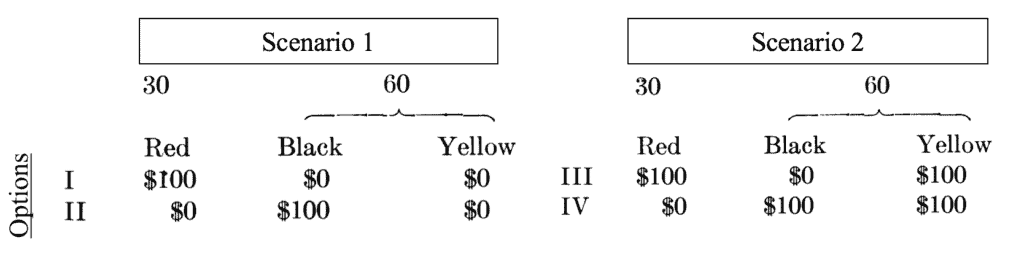
Many people choose Option I from scenario 1 and Option IV from scenario 2, but this combination of choices is inconsistent. They imply that the subject prefers to bet ‘on’ red rather than ‘on’ black by choosing I; and he or she also prefers to bet ‘against’ red rather than ‘against’ black by choosing IV.
In other words, the subject believes it is more likely for a red ball to be pulled than a black ball in scenario 1 and that it is more likely for a black ball to be pulled than a red ball in scenario 2 (because the probability of a pulling a yellow ball is the same for choices III and IV). These outcomes clearly illustrate the idea of preferring the devil you know.
In scenario 1, the subject who chooses I prefers the choice where he or she knows the chance of winning is 30%, even though the unknown proportion of black and yellow balls could be 60 black and 0 yellow, which would mean that choosing black would lead to a 60% chance of winning. In scenario 2, the subject who chooses IV prefers the choice where he or she knows the chance of winning is 60% even though the combination of red and yellow could lead to a higher than 60% chance of winning.
By choosing I and IV, subjects opt to avoid unknown risks (i.e. betting on the unknown proportion of black and yellow balls). Ambiguity aversion, as defined by Ellsberg, may help to explain some of this choice inconsistency.
Ambiguity Aversion
Agents exhibit ambiguity aversion when they prefer known risks over unknown risks. Ellsberg discusses ambiguity aversion as a potential reason for the discrepancies observed in the urn scenarios presented above. People prefer the option for which they know the probability of winning over the one for which they don’t.
It’s important to distinguish between ambiguity and risk aversion. With risk aversion, people tend to choose the option with a smaller payoff but a higher probability of occurrence. However, in these types of scenarios, they know the probability of occurrence for all the options. On the other hand, when situations are ambiguous, the probability of occurrence is unknown. As a result, people tend to choose the option where the probability is known in order to avoid ambiguity.
Calibration Theorem
The final theorem discussed here, the calibration theorem, has to do with risk aversion rather than ambiguity aversion. The theorem was proposed by Matthew Rabin in 2000 and “calibrates a relationship between risk attitudes over small and large stakes”, showing that “anything but virtual risk neutrality over modest stakes implies unrealistic risk aversion over large stakes”.
The typical model of risk aversion derived from the theory of diminishing marginal utility of wealth explains large-scale risk (“a dollar that helps us avoid poverty is more valuable than a dollar that helps us become very rich”), and it implies that people are risk neutral when stakes are small. However, the expected utility theory also implies that people would be approximately risk-neutral over large stakes as well (whereas economists often use this theory to incorrectly assume that people would be risk averse in the face of large stakes).
As an example, Rabin shows in the paper that someone who would turn down a 50/50 bet of losing $100 or gaining $110 would turn down 50/50 bets of losing $1,000 or gaining any sum of money. Additionally, a person who would turn down 50/50 bets of losing $1,000 and gaining $1,050 would turn down 50/50 bets of losing $20,000 or gaining any sum. Of course, these seem like unreasonable levels of risk aversion.
Rabin explains the theorem further with mathematical examples in the paper, but his main message is that the expected utility theory assumes a very rapid rate of money utility deterioration and that the miscalibration of expected utility theory is an explanation for why modest-scale risk aversion is observed in human behavior.

