The concept of time inconsistency can help us understand why some people procrastinate at work until the last minute, why we often buy gym memberships and don’t end up going, and much more. Time-inconsistent decision-makers are commonly described as having ‘different selves’ at certain points in time that make inconsistent choices with each other.
For example, if people are given the following two choices: $500 today or $505 tomorrow and $500 in a year or $505 day in a year and one day, the time-consistent answer would be to choose either $500 in both cases of $505 in both cases. However, many people will choose $500 today and $505 in a year and one day from now. This combination of choices is inconsistent because both choices involve the exact same differences ($5 and one day) and thus should result in the same choice regardless of time.
Discounting
These inconsistent choices can be attributed to a need for immediate satisfaction, or in other words, present bias. Decision-makers are often biased toward their present selves and thus put a greater weight on the choice that will currently benefit them. Those people discount the benefits of choices increasingly with time. In other words, they put less and less weight on the benefits of a choice the farther out into the future that choice gets.
Saving for retirement (or lack thereof) provides a great example of this discounting. The benefits of saving for retirement early are clear: compound interest allows retirement savings to grow almost exponentially. However, many people who have the means to do so don’t start saving for retirement until much later in their lives, when the benefits of compound interest are much smaller.
In these cases, young people significantly discount the benefits their future retired self will receive from saving more now because it is difficult to imagine that future self. As a result, they choose to benefit their present self by spending the money instead of saving it. Richard Thaler has significantly advanced the field of behavioral economics and has focused much of his research on why people don’t save for retirement and how to improve that.
Quasihyperbolic and Geometric Discounting
Decision-making and discounting can be described mathematically. A general formula for time discounting is: Ut = D(0)ut + D(1)ut+1 + D(2)ut+2 + … where Ut is the present utility, D(s) is the factor by which the current or future benefit is discounted, and ut+s is the utility of the reward in that period. The formula also helps determine the rate at which people are willing to shift rewards over time.
Geometric discounting gives a model for time-consistent discounting. In this case, the decision-maker is always willing to shift rewards over time at the same rate. In other words, the decision-maker can weigh benefits consistently relative to their time of occurrence. For example, a person whose decisions follow this formula would desire neither immediate nor delayed gratification.
Time-inconsistent discounting is not geometric, and researchers have discovered over time that quasihyperbolic discounting more realistically accounts for behavioral patterns and is better for analysis and applications. In this type of discounting the entire future is discounted by a factor b < 1, indicating that people value rewards much more now than in the future.
Quasihyperbolic discounting more accurately represents behavior because rewards much farther in the future are discounted very similarly to each other (or equally) due to the b factor. The following figure is an example of the different types of discounting and how the discount factor changes choices over time (substituting age for time).
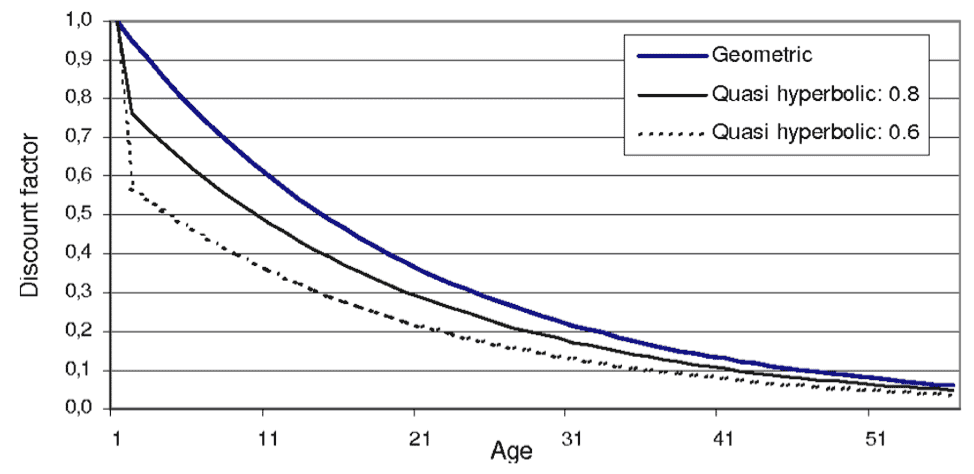
Discounting Example
The following example provides a more concrete picture of discounting. In this example, assume that there are three weeks, and in each of the first two weeks the decision-maker must decide whether to go to the gym in weeks 2 and 3. If she goes to the gym, she will receive the benefit listed in the first row, but if she doesn’t go, she will receive different benefits, listed in the second row. Also assume that b = 0.5.
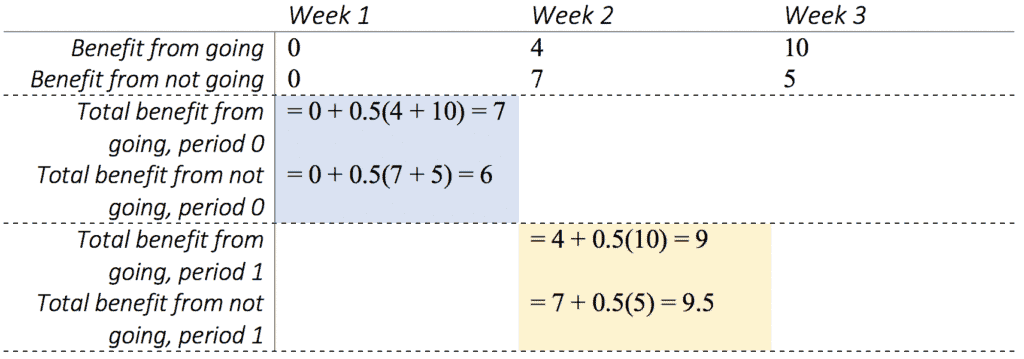
The decision-maker needs to choose whether to go to the gym in the next two weeks based on the sum of the benefit now and the discounted future benefit. These decisions are evaluated based on quasihyperbolic discounting, where all future benefits are discounted by the b factor.
In week 1, she will sum the total benefits of going to the gym for the next two weeks and discount all future benefits by b = 0.5 (shown in blue in the above table). Since the total benefit from going (7) is greater than the total benefit from not going (6), she will want to go to the gym in both weeks 2 and 3.
However, when week 2 rolls around, she will re-evaluate the choices based on the benefits from week 2 and the discounted benefits from week 3 (shown in tan in the above table). In week 2, the total benefit from not going (9.5) is greater than the total benefit from going (9), so she will not go to the gym even though from the beginning she knows it will be better for her.
Types of Time-Inconsistent Decision-Makers
While many people exhibit time-inconsistent behavior, they can be categorized even further into specific types of time-inconsistent decision-makers: sophisticated (‘soph’) and naïve (‘naif’). A soph recognizes that he or she will likely make present-biased decisions and correctly anticipates future decisions. A naif believes that he or she will always follow through on commitments and will never make a present-biased decision. However, it is expected that naifs will learn over time and become a soph (though this is not always the case). These differences lead to variations in the behavior of individuals in each group.
For example, since sophs recognize their inability to properly make decisions and follow through on them, they will often seek out commitment devices. These strategies help sophs follow through on decisions today that would benefit their future selves. A typical commitment device for a dieter who knows that they’ll want chocolate at night is to throw away all the chocolate in the house before they even have a chance to eat it at night. Similarly, smokers might throw away all their cigarettes, so their future self won’t have the option to smoke.
On the other hand, naifs see no need for commitment devices because they believe that they’ll always make decisions consistent with time. In fact, commitment devices have costs but no benefits to the naïve decision-maker. The decision-maker would have to pay the initial investment, but since they believe they’ll follow through on the commitment even without the device, they also believe that they would receive no benefit from the commitment device.
In the earlier example, commitment devices could come in handy. In week 1 the decision-maker knows that it is better for her, in the long run, to go to the gym both weeks, but if she is sophisticated, she also knows that when next week comes she won’t go. Thus, she would benefit from purchasing a commitment device, as long as the benefits outweigh the costs.
Sources:
Quasihyperbolic discounting section adapted from a lecture by Stanford professor, Marcelo Clerici-Arias


Its very interesting how people make choices, i particulary think thay people prefer chouse decision that give them quick benefict because is more safe and truth to have it, and people prefer wate more time when the benefits are in the future because is less safe and maybe think whay not wait more if i have to wait anyway.
Coincido con Anhelo Castillo en que las personas prefieren la decisión de elección que les da un beneficio económico rápido porque es más “seguro”; sobretodo porque la cultura occidental promueve y valora la inmediatez, y ademas, por los vaivenes económicos que atraviesa la economía mundial (sobre todo los países subdesarrollados, en la que la devaluación del dinero crece… por lo tanto, ¿para que esperar a recibir un poco más de dinero si es probable que para esa fecha futura ya no tenga la validez necesaria para justificar su espera?)
Se escucha en el argot popular que a las mujeres nos encantan las ofertas, es usual ver estos letreros en almacenes que venden artículos femeninos, pienso que también hace parte de la cultura y del mercadeo que atrapa, prácticamente es inmediato el comportamiento de adquirir el objeto, esto seria un sesgo actual. El ejemplo del gimnasio pasa con frecuencia que ofrecen grandes descuentos la persona se ilusiona con el precio y las ventajas de ir al ginmasio, pero si muchas veces terminan por ir pocas veces, en ultimas sale mas costoso, realmente el tema del comportamiento es complejo, esto se trata de un tomador de decisiones inconsistente en el tiempo sofisticado, donde se piensa inicialmente que se tendrá el control de la acción futura y realmente no ocurre así.
Most people enjoy the now, saving for a pension at a young age seems not to be important; because of short-termism, they want the benefits NOW! or because of ‘time inconsistency’ its always not now but later or i’ll do it another time.
Es muy difícil los modelos de vida idealizados por los medios de comunicación y la cantidad de ofertas que se ponen a disposición de las personas de bajos recursos, generan unas formas de vida inmediatista, de consumo, de no planear , no ahorrar, no educarse. Las personas quieren estados asistencialistas, que estos subsidie sus carentes formas de vida, de algo de los que se aprovechan los grupos económicos, los políticos corruptos, el gobierno mediocres; para crear programas carentes de proyección y de trascendencia para generar poblaciones consientes y responsables de su ciudadanía; donde todo esto un circulo vicioso que no acaba.