The concept of “returns to scale” describes the rate of increase in production relative to the associated increase in the factors of production in the long run. In other words, it describes how effectively and efficiently—in other words, profitably—a particular company or business is producing its goods or services. At this point, all factors of production are variable (not fixed) and can scale up. Therefore, the scale of production can be changed by changing the quantity of all factors of production.
Conceptualizing “returns to scale” is an effort to specifically understand how production increases relative to factors contributing to production. Production functions typically include capital as well as labor.
The difference between economies of scale and returns to scale is that economies of scale show the effect of an increased output level on unit costs, while the return to scale focus only on the relation between input and output quantities.
The Law of Returns to Scale

Returns to scale are actually governed by three separate laws:
1. Law of Increasing Returns to Scale
If production increases by more than the proportional change in factors of production, this means there are increasing returns to scale.
2. Law of Constant Returns to Scale
If production increases by the same proportional change as all factors of production are also changing, then there are constant returns to scale.
3. Law of Diminishing returns to Scale
If production increases by less than that proportional change in factors of production, there are decreasing returns to scale.
Increasing Returns to Scale
Increasing returns to scale happen when all the factors of production are increased; at this point, the output increases at a higher rate.
For example, if all inputs are doubled, the overall output will increase at more than twice the rate—this is the increase in output relative to inputs that “increasing” describes.
Diminishing Returns to Scale
Decreasing or decreasing returns to scale are taking place when all the factors of production increase in a given proportion, but the output increases at a lesser rate than that of the increase in factors of production. To compare this to increasing returns to scale: for decreasing returns to scale, increasing inputs leads to smaller increases in output; for increasing returns to scale, increasing inputs leads to the opposite—larger increases in output.
For example, if the factors of production are doubled, then the output will be less than doubled.
Constant Returns to Scale
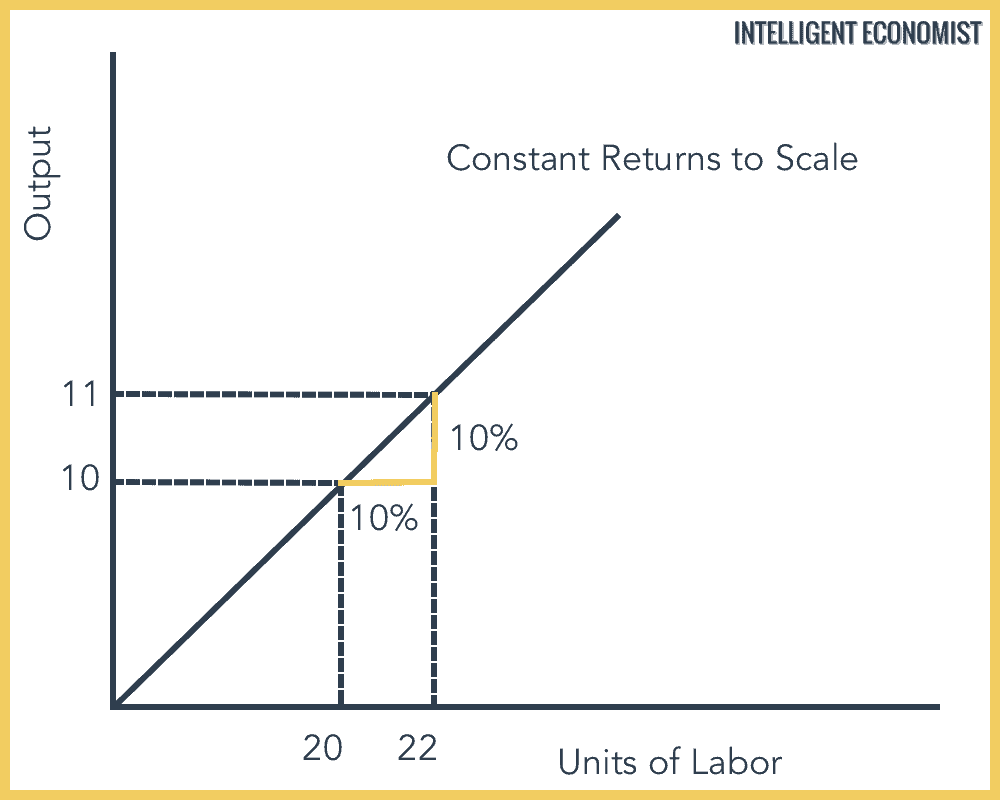
Constant returns to scale occur when the output increases in exactly the same proportion as the factors of production. In other words, when inputs (i.e. capital and labor) increase, outputs likewise increase in the same proportion as a result. As an example of constant returns to scale, if the factors of production are doubled, then the output will also be exactly doubled.
Here is a graph representing the concept of constant returns to scale—the increase is represented by a straight line at a 45-degree angle since increases on the X-axis (inputs—units of labor/capital) are always equal to increases on the Y-axis (overall output).
Note that returns to scale take place over the long run, during which time labor and capital are typically variable.
Constant Returns to Scale & Economies of Scale
In a situation where a firm experiences constant returns to scale, there are likely to be fewer economies of scale, but this is balanced out by fewer diseconomies of scale. Nevertheless, it is still possible for a firm to enjoy economies of scale while experiencing constant returns to scale, because they may experience bulk buying economies (purchasing larger quantities of inputs lowering their cost per unit) and financial and marketing economies.
Multipliers for Returns to Scale
Our multiplier, in this case, will be m. If we double our inputs of capital and labor, then m = 2. The question is whether our outputs are greater than double, double exactly, or increase by less than double. Our three forms of return to scale (described above) can be described as such in these terms:
- Increasing returns to scale: When the input increases by m, and the output increases by greater than m.
- Constant returns to scale: When the input increases by m, and the output also increases by exactly m.
- Decreasing returns to scale: When the input increases by m, and the output increases by less than m.


Why do firms need to stop adding more inputs at a point where there is a constant return to scale?
Constant returns to scale is the situation when you employ some amount of input that gives the same amount of output. It means you are already employing a sufficient amount of inputs that your production is large and you are producing at a low cost. This means your company is efficient and earning more profit which is a common objective of any firm. This is why you need to stop adding more inputs when you (as a producer) realize constant returns to scale.
Otherwise, if you add more input you will experience decreasing returns to scale because the more input you employ (large quantity of raw materials, labour, etc), the complex it becomes and the efficiency of your company declines than before making less profit for your company.
Doesn’t your vertical axis show a 20% increase in output (while your horizontal shows a 10% increase). You have a 45 degree angle (or at least it appears so), but your axes are calibrated differently.
You’re right about the 10% increase. It should be 20%.
Huh? On the vertical axis, the output went from 10 to 11; an increase of 1.
1/10 = 10%.
He is right with the 10% increase in the output…what matters is the percentage increase and not the change in the number of units
(11-10)/10 *100 = 10%
Apart from economies of scale what are some of the causes of constant returns to scale