Cyclical Unemployment

Put simply, cyclical unemployment is a form of unemployment that occurs as a result of an economic decline or periods of negative economic growth in a business cycle. Other names for cyclical unemployment are “deficient-demand” or “Keynesian unemployment“

What these three terms have in common is the main factor causing unemployment demand. “Deficient-demand” means that the aggregate demand in an economy is lower than the aggregate supply, which would lead to a surplus of products on the market. In other words, we are looking at an economy in which people are less likely to consume, for any given reason. The ultimate outcome of this is unemployment, for reasons we explore later on in this article.

In situations of economic decline, economists and policymakers focus on creating tools to reduce the adverse effects of cyclical unemployment as effectively as possible. These tools are used to stimulate the economy and to prevent serious economic hardship to the extent of, say, the Great Depression.

Contents show

Key Takeaways:

In this article, we will explore the concept of cyclical unemployment in-depth, examine its causes and effects, and compare it to the related but distinct idea of structural employment. We will also investigate the answers to the following questions:

What does cyclical unemployment mean, and where does it occur in the business cycle?
What is the chain of events that causes cyclical unemployment?
What do businesses do during periods of economic downturn that increase cyclical unemployment?
What are some examples of cyclical unemployment in the real world?
Why is the concept of cyclical unemployment important to economists and consumers?
How is the problem of cyclical unemployment typically managed by economists and policymakers?

Causes of Cyclical Unemployment

Cyclical unemployment happens after an economy enters a period of contraction—that is to say, an economic decline or recession.

Cyclical unemployment can be described as a chain of events that starts with a recession. The chain goes as such:

First, when an economy goes into a recessionary phase, there is a decrease in demand. As in any recession, consumers are overall less likely to spend.
As demand decreases, businesses are forced to lay off workers to make up for losses in sales and reduce expenses.
They continue to do this until supply decreases to meet the new demand.

The workers who were laid off as a direct result of the decreased demand are the population we look at when we observe cyclical unemployment. Consider the following graph:

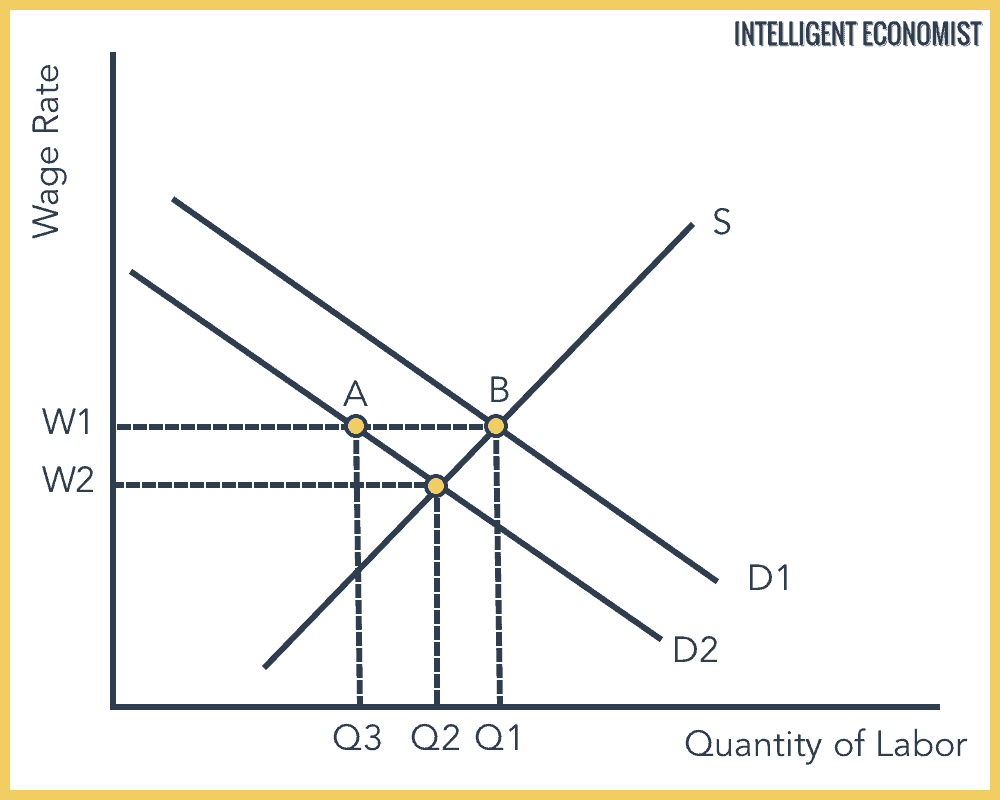
As you can see, as demand for labor decreases from (D₁) to (D₂), there becomes an excess of workers who cannot find jobs at the same wage rate as before. Points AB is the increase in unemployment. The new market equilibrium is W2 and Q2. So, those workers become unemployed as a direct result of a contraction in the economy.

In the next section, we will discuss environments in which high rates of cyclical unemployment are most likely to occur.

Setting the Stage for Cyclical Unemployment

Earlier on in this article, we learned that cyclical unemployment is a natural result of economic downturns. But, some of these downturns give rise to higher rates of cyclical unemployment than others. If that is the case, what kinds of economic environments are most likely to lead to cyclical unemployment?

To answer this, we can look at the behavior of most companies. Since companies are reluctant to fire workers and lose the investment they’ve placed in them, cyclical unemployment typically doesn’t happen until the economy is doing quite poorly. In these situations, entire companies are more likely to go under, and cyclical unemployment will increase precipitously at that point. From this, we can conclude that cyclical unemployment is most likely to happen after significant and long periods of recession. Here’s what that process looks like:

When companies go out of business entirely due to an economic recession, the workers at that company become unemployed.
With fewer goods being ordered, production eventually decreases to match the lowered level of demand.
There is less demand for labor as a result, since fewer jobs are available, and more workers become unemployed.
This also creates negative multiplier effects; with lower levels of production in one industry, related industries are also affected, resulting in decreased demand.
- One example of this might be the cleaning services that would have cleaned the offices that have now closed due to lowered production levels. The cleaning services lose business, and as a result, will have a decreased need for labor. To continue the chain reaction, the workers at those cleaning services will end up unemployed as well.
When negative growth happens, companies attempt to lower their wage-related costs by hiring fewer new employees than they would during a healthier economic period.

As you might expect, the relationship between cyclical unemployment and recessions also exists in reverse. When the economy reaches a healthier state of growth, companies will hire more workers, thereby reducing this kind of unemployment.

Effects of Cyclical Unemployment

Now, let’s discuss what kinds of things after cyclical unemployment increases. In situations of significant cyclical unemployment, it may be difficult to know whether the problem requires just a bit of economic tweaking, or if it is a problem endemic in the structure of an economy itself. This dilemma plagues the thoughts of economists and policymakers in times of significant economic hardship and unemployment.

Here are some of the issues caused by cyclical unemployment as explored in the article “Unemployment: Causes and Cures” by David Aaron:

Long-term cyclical unemployment may shift into structural unemployment (discussed later in the article)
The increase in radical political ideologies, such as fascism
Young workers entering the labor market from school will be more likely to fall into unemployment and stay there
One of the biggest and most paradoxical problems of cyclical unemployment is that it depends on employers to lay off workers in order to allow the economy to regain equilibrium. This paradox means that some countries have to resort to encourage employers to lay off more workers, and even to reduce employment protections.
Effects of cyclical unemployment typically compound without some form of intervention, such as from governmental policy.

Cyclical Unemployment Examples

As a current example, the effects of Covid-19 has launched the U.S. and many other countries into the beginnings of a global economic recession. As mentioned earlier, periods of recession bring about certain levels of cyclical unemployment, usually related to the severity and duration of the recession. Observe the following chart:

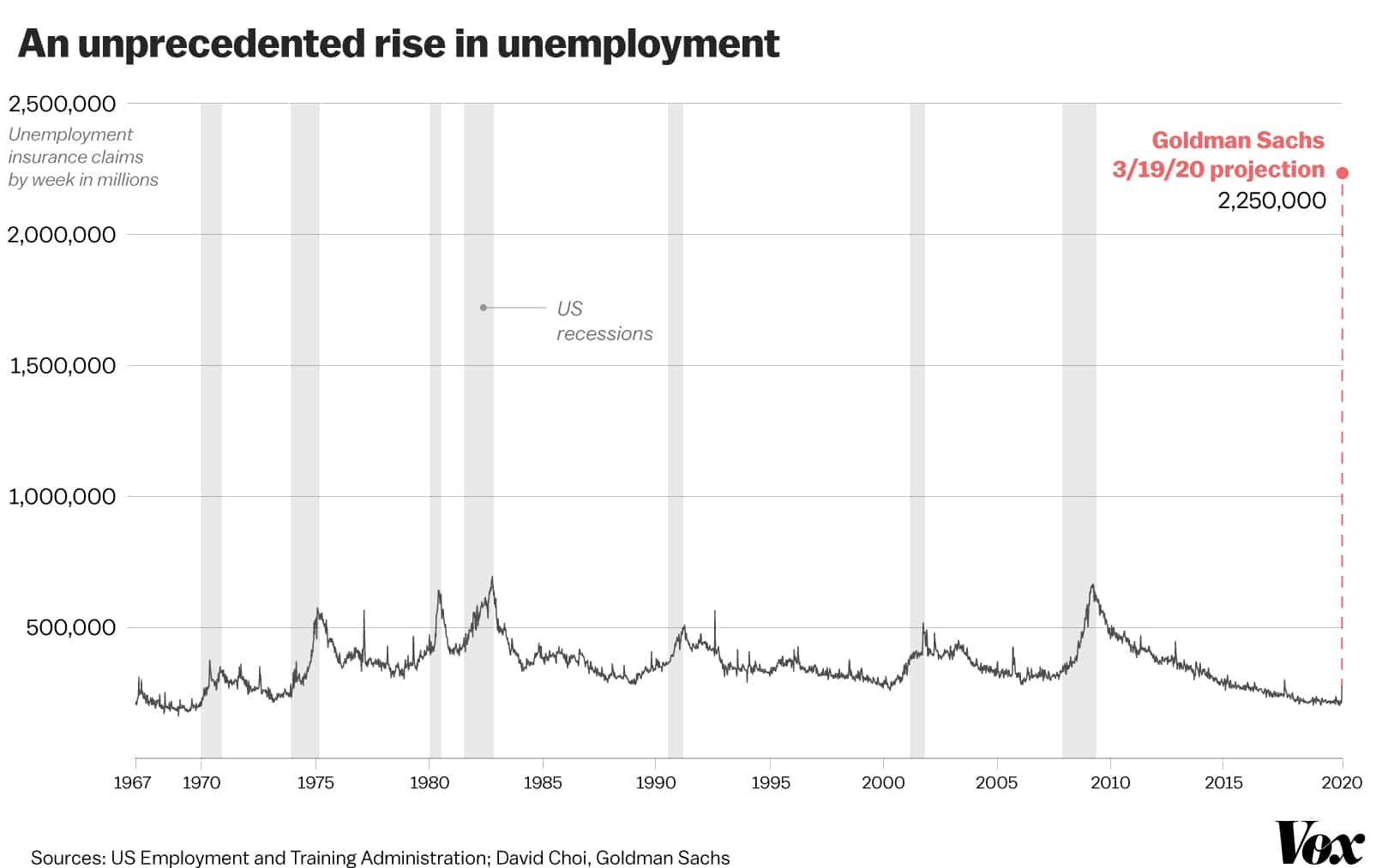
Covid-19 US Unemployment 2020 — Source: Vox

We can see that, though there are periods of unemployment peaks and valleys that exist outside of recession times, unemployment significantly increases during recessions. The Goldman Sachs projection for the number of unemployed Americans, about 2.25 million, is supported by the following chart:

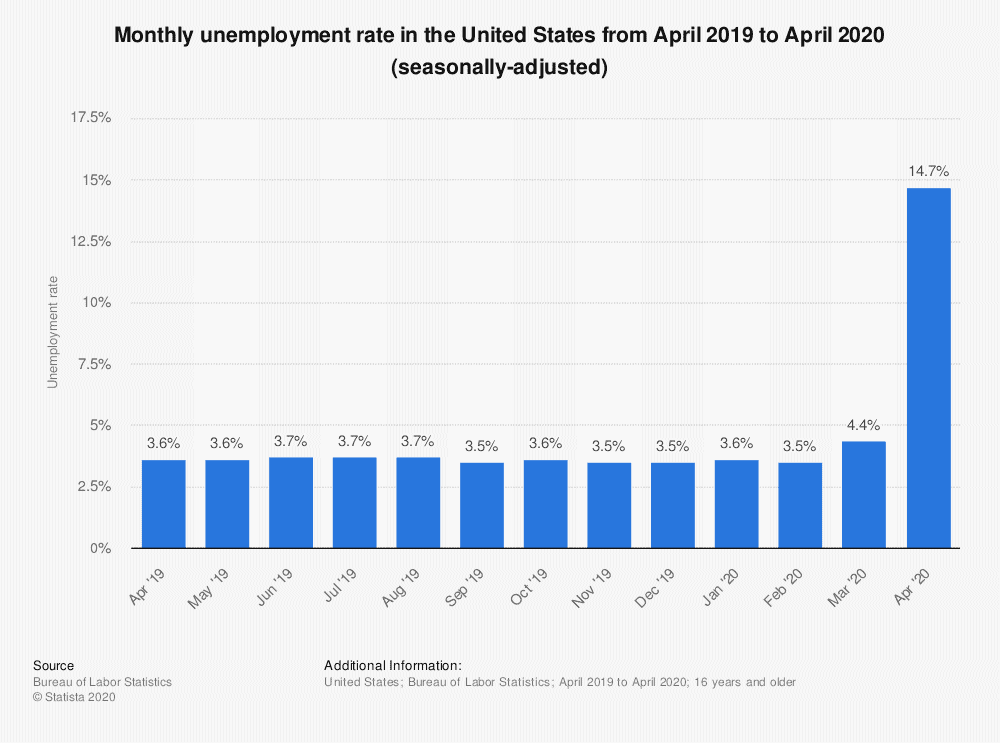
Monthly unemployment rate in the United States from April 2019 to April 2020 — Source: Statista

This seasonally adjusted bar graph represents the unemployment rate from April 2019 to April 2020. We can see that 14.7% of the U.S. labor force is reported to be unemployed. This would suggest that a staggering amount of unemployment resulting from the current recession is cyclical.

We don’t have to look back very far to find other examples of economic declines in our lifetime, and they have all come with varying levels of cyclical unemployment. Often, they have been triggered by stock market crashes. Two of the notable examples of this are the stock market crash of 1929—which lead to the infamous Great Depression—and the 2008 financial crash which preceded the Great Recession. Crashes lead to recessions by contributing to widespread economic anxiety and fear, as well as a lack of trust that the economy will function reliably.

A more industry-specific example of cyclical unemployment might be workers who build homes. When the economy goes through a period of negative growth, consumers have less money to spend. Thus, demand falls for new homes, making companies that would typically hire these laborers more reluctant to do so, since it would no longer be profitable. Many of these workers who would previously have been employed during periods of high economic growth and high demand for new homes will become unemployed.

What is Structural Unemployment?

Structural unemployment is a concept that is related to, but distinct from, cyclical unemployment. While cyclical unemployment happens as a result of economic contractions in the business cycle, structural unemployment happens due to a shift in the labor market composition. As time goes on, the labor market transforms to accommodate new technologies, policies, environmental needs, etc. This transformation will inevitably cause other job sectors to naturally phase-out. Structural unemployment is a result of certain jobs becoming unavailable permanently due to its lack of relevance in a transforming economy.

When does Cyclical Unemployment become Structural?

How exactly are cyclical and structural unemployment related? It turns out that in economies under prolonged distress, cyclical unemployment may transition into structural unemployment. For example, a worker who gained competency in computer programming in the late 1990s may lose their job as a result of the 2007-2009 financial crisis. When the economy recovers, however, they find that the skills they were trained in are no longer viable in the job market. This is an example of cyclical unemployment, which has become structural in nature.

Other Forms of Unemployment

Economists describe several forms of unemployment, cyclical and structural unemployment being just two examples. Other types of unemployment include institutional and frictional unemployment. Each of them has different causes and manifest differently.

Structural unemployment, for instance, is not affected by the ups and downs of the business cycle; instead, it is a product of underlying (structural) changes in the economy. Similarly, frictional unemployment is different from cyclical unemployment in that it can occur even in a healthy economy. However, it is important to note that only cyclical unemployment cannot occur at the highest point of the business cycle’s expansion phase, although the other kinds of unemployment can.

Seasonal Unemployment

The two might sound synonymous, but cyclical and seasonal unemployment are two distinct phenomena. Cyclical unemployment is linked to the patterns of the business cycle. In contrast, seasonal unemployment is connected to the changes in demand associated with seasonal changes (summer vs. winter, for example). Workers who experience seasonal unemployment are workers who were hired for a season-dependent job. For instance, in 2019, the private shipping and logistics company UPS hired nearly 100,000 workers to meet the holiday season rush. Only 35% of those workers were expected to become permanent UPS workers, meaning that the remaining 65% became seasonally unemployed.

Finding the Cyclical Unemployment Rate

We’ve talked about how cyclical unemployment is caused, and how it differs from other kinds of unemployment. Now, let’s find out how to calculate the rate of cyclical unemployment in any given economy.

The easiest way to determine the cyclical unemployment rate is to look at the excess job loss during the trough (lowest point) of the business cycle. The formula is constructed by taking the difference between the unemployment rate at the business cycle’s peak (highest point) and trough. It looks like this:

Cyclical unemployment rate = Unemployment rate at peak – Unemployment rate at trough

Another way to calculate the cyclical unemployment rate is to separate it from the other forms of unemployment that are happening at the same time: frictional unemployment and structural unemployment. That equation looks like this:

Cyclical unemployment rate = Total unemployment rate – (Frictional unemployment rate + Structural unemployment rate)

Those are just two ways of many, and they each have varying levels of accuracy. Still, they are useful tools in determining the extent of cyclical unemployment in an economy.